If, in some cataclysm, all of scientific knowledge were to be destroyed, and only one sentence passed on to the next generations of creatures, what statement would contain the most information in the fewest words? I believe it is the atomic hypothesis (or the atomic fact, or whatever you wish to call it) that all things are made of atoms—little particles that move around in perpetual motion, attracting each other when they are a little distance apart, but repelling upon being squeezed into one another. In that one sentence, you will see, there is an enormous amount of information about the world, if just a little imagination and thinking are applied.
R. Feynman (Lectures on Physics)
La frase es de las famosas Lectures on Physics, de Feynman, cuya publicación pronto cumplirá 50 años. El Capítulo en que aparece está también recogido en Seis piezas fáciles. La he recordado estos días al tomarla como punto de partida en unas notas de viaje de una excursión del átomo al Higgs que, aunque no escritas para el blog, es posible que se publiquen también aquí.
Es dificil no estar de acuerdo con Feynman. En este post y en el que le seguirá pretendo dar dos ejemplos de cómo mediante solamente observaciones muy sencillas, el hipotético «miembro de la siguiente generación de seres» que hubiera tenido la suerte de recibir el mensaje de Feynman, podría en efecto, aplicando un poco de imaginación y de pensamiento, tener una estimación razonablemente precisa del tamaño lineal de las «unidades mínimas de la materia».
En la antigüedad se había observado que una pequeña cantidad de aceite, vertida sobre la superficie de un cuenco, el agua de un estanque, o en el mar, inhibía las pequeñas ondulaciones y daba como resultado una superficie mucho más lisa y tranquila, incluso transformándola en un espejo. Plinio lo menciona. Hacia 1770, Benjamin Franklin se interesó por el asunto de una manera casual —mientras viajaba en barco, notó que entre las estelas de otros barcos con los que se cruzaban, algunas tenían las aguas muchísimo más tranquilas que otras—. Preguntó al capitán, que le respondió, como si todo el mundo lo supiera, que eso era lo que ocurría cuando vertían al mar el agua con grasa que resultaba al limpiar los útiles de cocina. Franklin, que había leído a Plinio, resolvió investigar el asunto experimentalmente. Y estando en Londres, comprobó que una muy pequeña cantidad de aceite de oliva vertida en un estanque se extendía casi de inmediato hasta cubrir una superficie relativamente grande. En esta zona, aunque la capa de aceite resultara invisible directamente, su presencia se infería de la ausencia casi completa de ondulaciones, que sin embargo se mantenían en la región adyacente.

El estanque de Clapham Common, antes y después de haber vertido una pequeña cantidad de aceite. Nótese como en la zona cubierta por aceite se suprimen las ondas de capilaridad, inducidas en el agua por el viento y mantenidas por la tensión superficial. Crédito de la imagen: C. H. Giles
Al verter el aceite, la superficie así protegida crecía de manera casi instantánea hasta un valor máximo, sin que luego se extendiera más. Repitió el experimento varias veces, en varios estanques, siempre con el mismo resultado. En concreto, los datos que Franklin da para el experimento en un estanque de Clapham Common indican que con una cucharita de té de aceite (cuyo volumen podemos estimar en unos 2 cm3), la zona que quedaba lisa como un espejo ocupaba una superficie estimada de medio acre, que era la cuarta parte de la superficie total del estanque. Franklin publicó sus observaciones en las Philosophical Transactions of the Royal Society en 1774 (B. Franklin, Phil. Trans. R. Soc. London, 1774, 64, 445).
Imaginemos un para-Franklin que hubiera recibido la frase de Feynman e hiciera profesión de fe en el mensaje de que todos los materiales están formados de unidades básicas, del mismo tipo. Consecuentemente, no entraremos en detalles sobre la distinción entre átomos y moléculas, ya que lo que se pretende es simplemente, tener una estimación fiable del tamaño de tales hipotéticas unidades mínimas.
Este para-Franklin realiza el experimento y observa que el aceite se extiende inmediatamente hasta que cubre una cierta extensión, que una vez establecida ya no aumenta más. La interpretación es casi inevitable con la simple hipótesis de que lo que se extiende por el agua es una película monomolecular de aceite. Así se explica perfectamente que no pueda extenderse más. Un test de esta hipótesis sería ver que la superficie cubierta es proporcional a la cantidad de aceite vertida, algo que parece que el Franklin real también advirtió. Una vez puesta la cuota de imaginación que Feynman da por supuesta, el resto es un simple cálculo: supongamos que las moléculas de aceite son cubitos de lado L. Sea Vc el volumen del aceite vertido (cuyo valor estimamos en 2 cm3). Como cada molécula ocupará un volumen del orden de L3, el número de moléculas de aceite Nc que podemos esperar tener en la cucharilla es Nc = Vc/L3. Naturalmente, este número no le podemos contar, de manera que esta ecuación, ella sola, no nos dice nada sobre L. Pero una vez extendido sobre el agua, el aceite ocupa una lámina de superficie S cuya altura es la de una molécula L, y cuyo volumen es por tanto S L. Parece razonable admitir que el volumen del aceite vertido deba conservarse cuando se desparrama, y por tanto los dos volúmenes han de ser iguales, Vc = S L y naturalmente, de aquí podemos obtener una estimación del tamaño lineal de las moléculas de aceite, L
Vc/S. Basta informarse de que un acre son 4046,86 m2 para concluir el valor de L
2 (10-2)3 m3 / 2023,43 m2= 9.88
10-10 m. De manera que el orden de magnitud del tamaño de las hipotéticas `moléculas de aceite’ es de 10-9 m, esto es, un nanometro. De aquí se puede obtener la estimación de cuantas moléculas de aceite contiene la cucharita, que resulta en el valor Nc
2
(10-2)3 m3 / (10-9)3 m3 = 2
1021; el lector reconocerá la cercanía con el número de Avogadro, que se obtendría claro está si tomáramos no una cucharita de aceite sino un mol. El aceite de oliva es una mezcla, pero su fracción dominante es la trioleina, un derivado del ácido oleico, cuya masa molar es de 885 gramos por mol. Como la densidad del aceite es menor que la del agua, la masa de nuestra muestra sería algo menor de 2 gramos, y vemos que se necesitarían unas 500 de nuestras cucharitas para completar un tal «mol» lo que nos daría un número de «moléculas» de 500
2
1021
10
1023, que corresponde correctamente al orden de magnitud del número de Avogadro; por supuesto esta última determinación no habría sido posible para nuestro para-Franklin, ya que requiere conocer aparte la masa molar de la sustancia.
Claro está, a esta derivación se le pueden buscar todas las cosquillas que se quiera. Aparte de su anacronismo, el aceite no es un compuesto único, sino una mezcla. Sus «moléculas» no son perfectos cubitos de un juego infantil de construcción. Etc etc. Lo que no obsta para que la derivación sea esencialmente correcta: nuestro imaginario para-Franklin bien pudiera haberla completado. A finales de los 1960, C.H. Giles repitió la experiencia en el mismo estanque (C. H. Giles, Chem. Ind., 1969, 1616), y tomó las fotografías que hemos reproducido más arriba, antes y después de haber vertido una pequeña cantidad de aceite.
Franklin estimó correctamente el grosor de la película, en el orden del nanometro, pero seguramente nunca imaginó que su observación contenía uno de los primeros germenes de la determinación del tamaño real de las moléculas.
En el próximo post hablaré de otra manera de hacer estas estimaciones, tomando también como punto de partida experiencias de la vida diaria pero que involucra a la física, pues la de hoy realmente no lo hace. Como desideratum, no estaría mal que de cada simple observación cotidiana de la naturaleza, intentáramos obtener información no-trivial sobre el mundo real.
Es decir, que aprendieramos a ir por la vida con los ojos abiertos. Pues como suele ocurrir, solo mirar no es suficiente para ver.
Este post es el primero de una mini-serie de tres posts. Si quiere saltar directamente a otro de la misma serie, puede usar los enlaces siguientes, directos a cada entrada.
El tamaño de las moléculas (II)
El tamaño de las moléculas (y III): Weisskopf y Waterston
La época en su música.
En 1749 Carl Philipp Emanuel Bach compuso el Magnificat Wq 215, que revisó varios años después, más o menos en las fechas en las que Franklin realizaba sus experimentos en Inglaterra. No podemos recrear la época, pero si sumergirnos en su ambiente sonoro, y para ello esta obra es una auténtica joya. Merece la pena escucharla completa; a mí me es difícil escoger una parte, y si tuviera que hacerlo seguramente sería el Deposuit potentes, (aunque el Fecit potentiam, que viene antes, en 18:35 es también espléndido, y el resto no difiere de la perfección de éstas dos partes en más del prototípico ).
Oyéndola, se comprende que a este hijo de Bach le llamaran en su época Bach el Grande, distinguiéndolo de su padre, Bach el viejo, quien estaba cayendo entonces en un olvido relativo del que le rescató para la posteridad Felix Mendelssohn en el siglo siguiente.



Pingback: Del átomo al Higgs IV: La electrodinámica cuántica y los primeros ejemplo de la teoría cuántica de campos | Una vista circular
Gracias miles por este post. Mi hija de 12 años está trabajando en su proyecto de ciencias y escogió este experimento. Como yo soy «literata» y no científica, encuentro cosas que no entiendo pero tu artículo me ha dado muchas luces.
Sin embargo seguimos atascadas y quisiera saber, si usted puede ayudarnos.
El experimento nos hace calcular primero el volumen de una gota de aceite de oliva flotando en un alambre (Midiendo el diámetro aproximado de la gota con una lupa y una regla). Luego, vertemos la misma gota, en una bandeja plana llena de agua a un centímetro de alto, donde previamente hemos esparcido polvo de tiza. La gota se vierte sobre el polvo de tiza flotante y se expande, formando un círculo perfecto que se puede ver nítido gracias al polvo de tiza de que lo dibuja (es facinante!).
Según el libro que sugiere el experimento, debemos medir el diámetro del círculo y calcular su volumen y su área…
En adelante, el libro no es claro y ahí estamos atascadas ya que no entendemos qué debemos hacer exactamente para calcular el tamaño de una molécula.
El libro dice: «Calculate the oleic acid´s volume and its area on the water. You can then determine the thickness of the layer and, therefore, the maximum height of an oleic acid molecule».
¿Cómo con los valores del volumen de la gota y del volumen y el área del circulo, podemos determinar el grosor y la altura de una molécula?… ¿Cómo medir el alto de una capa de aceite sobre el agua cuando es tan delgada?
Gracias de corazón por su atención.
Paola.
Paola, que chulo experimento. Espero que os salga muy bien y ambas disfrutéis aprendiendo.
Entiendo que lo que el libro sugiere es lo siguiente. El volumen de aceite de la gota inicial, que era una esfera, tras verterla sobre la superficie del agua contenida en la bandeja, se extiende en forma de un disco muy delgado que debes suponer, como en el post, que tiene de espesor el `tamaño’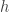 de una molécula de acido oleico (espesor que no conoces, y que es lo que tratais de calcular).
de una molécula de acido oleico (espesor que no conoces, y que es lo que tratais de calcular).
El volumen de ese disco de aceite debe ser igual al volumen de la gota que vertisteis (volumen que habéis calculado al principio tras medir el radio r y aplicar la fórmula del volumen de una esfera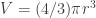 ). Pero tras verter el aceite, ahora el volumen de ese delgado cilindro se obtiene calculando primero el área del disco (cuyo radio R de nuevo has de medir con una regla, aplicar la relación que da el área del disco
). Pero tras verter el aceite, ahora el volumen de ese delgado cilindro se obtiene calculando primero el área del disco (cuyo radio R de nuevo has de medir con una regla, aplicar la relación que da el área del disco 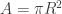 ) y multiplicar ese área por el espesor h del disco para obtener el volumen, que ahora es
) y multiplicar ese área por el espesor h del disco para obtener el volumen, que ahora es 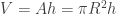 . He llamado r al radio de la gota esférica inicial, y R al radio del disco plano que queda sobre el agua.
. He llamado r al radio de la gota esférica inicial, y R al radio del disco plano que queda sobre el agua.
Claro, el espesor no puedes medirlo directamente, ya que es extraordinariamente delgado. Justamente la gracia del ejercicio es que, como los dos volúmenes, el de la gota inicial y el del disco de aceite una vez extendido sobre el agua deben ser iguales, lo que puedes hacer es calcular h. Despejando h en la igualdad entre los volúmenes , (aunque tu ya hayas olvidado eso de despejar, tu hija lo tendrá fresco) lo que encuentras es que h es el cociente entre el volumen de aceite en juego (el de la gota inicial) y el área del disco, cociente que está dado por
, (aunque tu ya hayas olvidado eso de despejar, tu hija lo tendrá fresco) lo que encuentras es que h es el cociente entre el volumen de aceite en juego (el de la gota inicial) y el área del disco, cociente que está dado por  .
.
Solo tenéis que cuidaros de expresar todas las distancias en las mismas unidades, seguramente lo mejor es expresar R y r en milímetros, y entonces el valor del tamaño h de la molécula de ácido oleico está dado en milímetros por . Debe dar un valor muy pequeño, como de una millonésima de milímetro.
. Debe dar un valor muy pequeño, como de una millonésima de milímetro.
PS. Me dan ganas a mí de hacerlo, y seguro que es fascinante ver el circulo perfecto. Estaría encantado si comentáis con el resultado que obtengáis. Sentiros como el propio Benjamin Franklin. La verdad es que a mí no se me había ocurrido que se podría hacerlo en casa.
Upsss!. En mi anterior respuesta había un factor 4 terriblemente incorrecto. Ya lo he corregido; ahora creo que está todo bien.